백준 2579번 계단 오르기 Swift
https://www.acmicpc.net/problem/2579
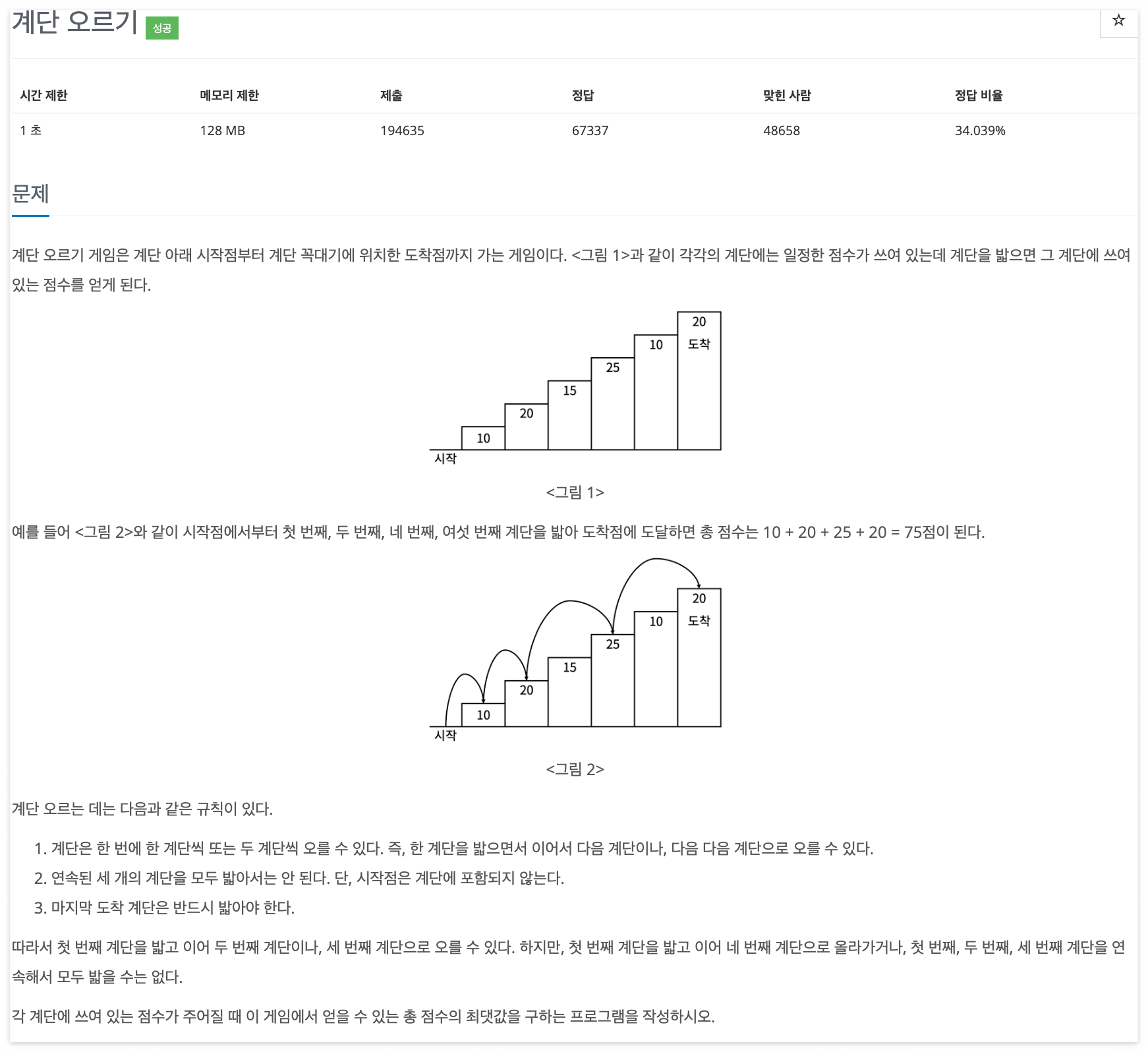
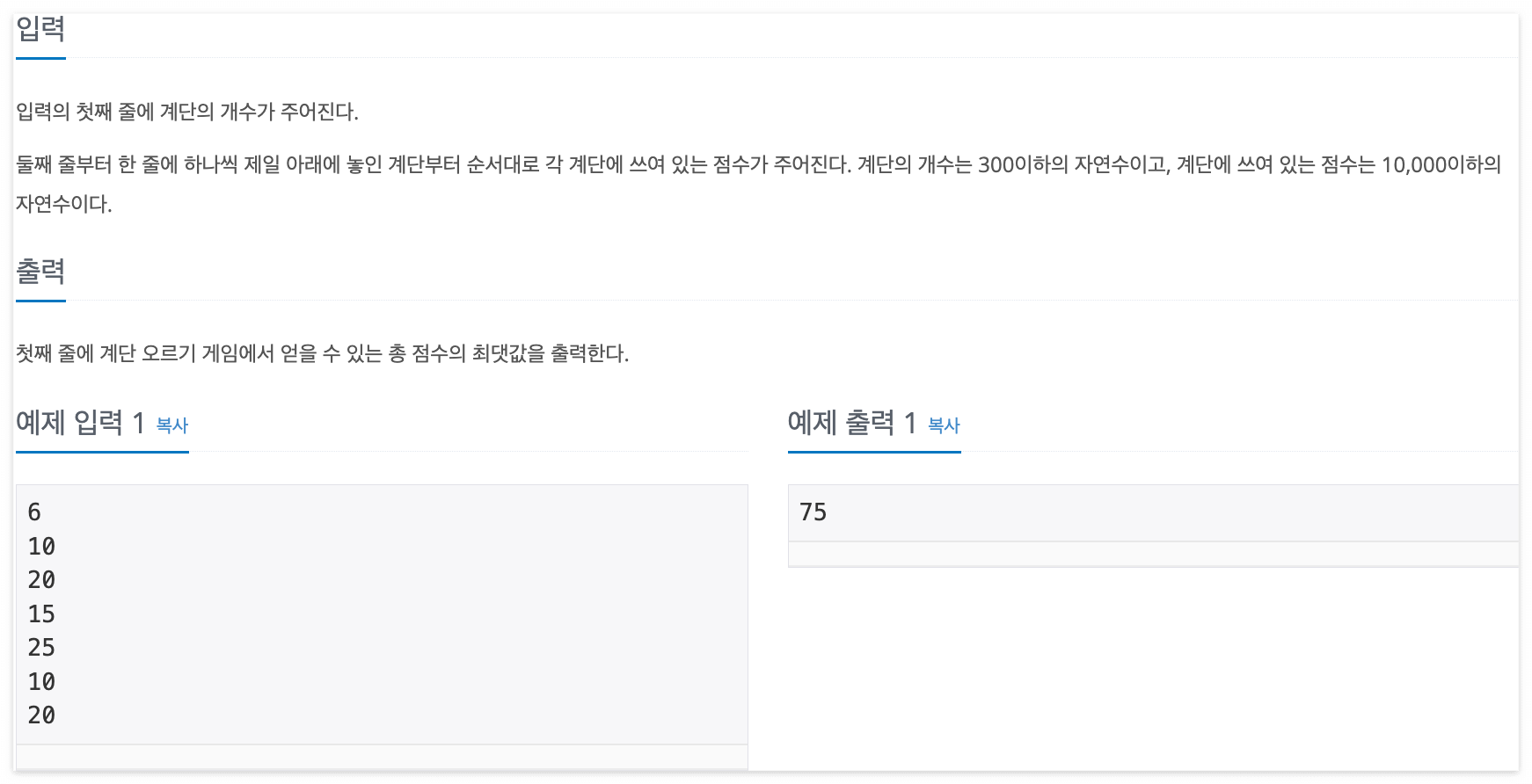
내 코드
let N = Int(readLine()!)!
var S: [Int] = []
var dp: [Int] = Array(repeating: 0, count: N)
for _ in 0..<N {
let element = Int(readLine()!)!
S.append(element)
}
dp[0] = S[0]
if N == 1 {
print(dp[0])
} else if N == 2 {
dp[1] = S[0] + S[1]
print(dp[1])
} else {
dp[1] = S[0] + S[1]
dp[2] = max(S[0] + S[2], S[1] + S[2])
for i in 3..<N {
dp[i] = S[i] + max(S[i-1] + dp[i-3], dp[i-2])
}
print(dp[N-1])
}Review
처음에는 아래 사진 처럼, 가지치기 형식으로 풀었습니다.
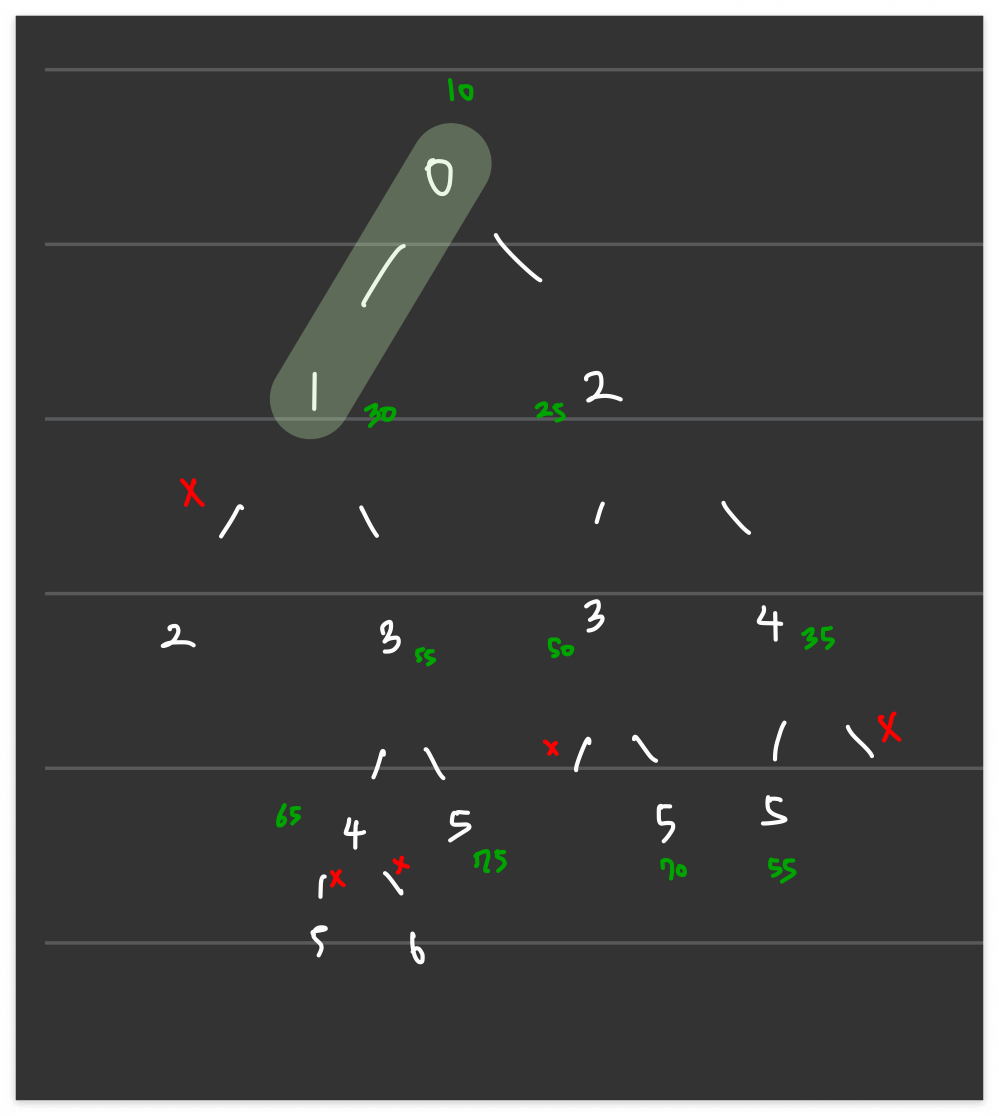
하지만 가지치기 단계에서 같은 연산이 반복되는 중복되는 과정도 있었기 때문에
다이나믹 프로그래밍(DP) 방식으로 생각을 돌렸습니다.
문제의 조건은 아래와 같습니다.
1. 계단을 오를 때, 한 번에 1 계단, 2 계단 씩 오를 수 있습니다.
2. 한계단씩 3번 연속으로 오를 수 없습니다.
예를 들어, 한 번에 계단 1, 2, 3을 모두 밟으면 안 됩니다.
점화식
마지막 계단을 밟기 전의 상황을 생각해 본다면
마지막 계단을 밟아야 하니까, 바로 전 계단(i-1) 또는 그전 계단(i-2)에서 올라와야 합니다.
바로 전 계단(i-1)에서 올라오는 경우를 좀 더 자세히 설명한다면
제가 계단 i-1에 있다고 가정해 볼 때, 그전에 계단 i-2는 밟을 수 없습니다.
왜냐하면 세 계단을 연속으로 밟으면 안 되니까요.!!
그럼 계단 i-3에서 i-1로 건너뛰어야 합니다. 그러고 나서 계단 i로 올라가요.
이렇게 하면 세 계단을 연속으로 밟지 않고, 마지막 계단도 밟을 수 있습니다!
이제 저희에게 필요한 dp 배열을 만들어 줍니다.
dp[i] 는 i번째 계단까지 올랐을 때의 얻을 수 있는 점수의 최댓값입니다.
먼저 초기값을 지정해 줍니다. (index는 0부터 시작합니다)
dp[0] 은 0번째 계단을 나타내므로 S[0]입니다.
dp[1] 은 1번째 계단에 올랐을 때의 최대 점수인데, 양수조건 이기 때문에 한 가지밖에 없습니다. 따라서 S[0] + S[1] 입니다.
dp[2] 는 2번째 계단에 올랐을 때의 최대 점수입니다. 2번째 계단을 오르는 경우의 수는 2가지 중에 큰 값입니다.
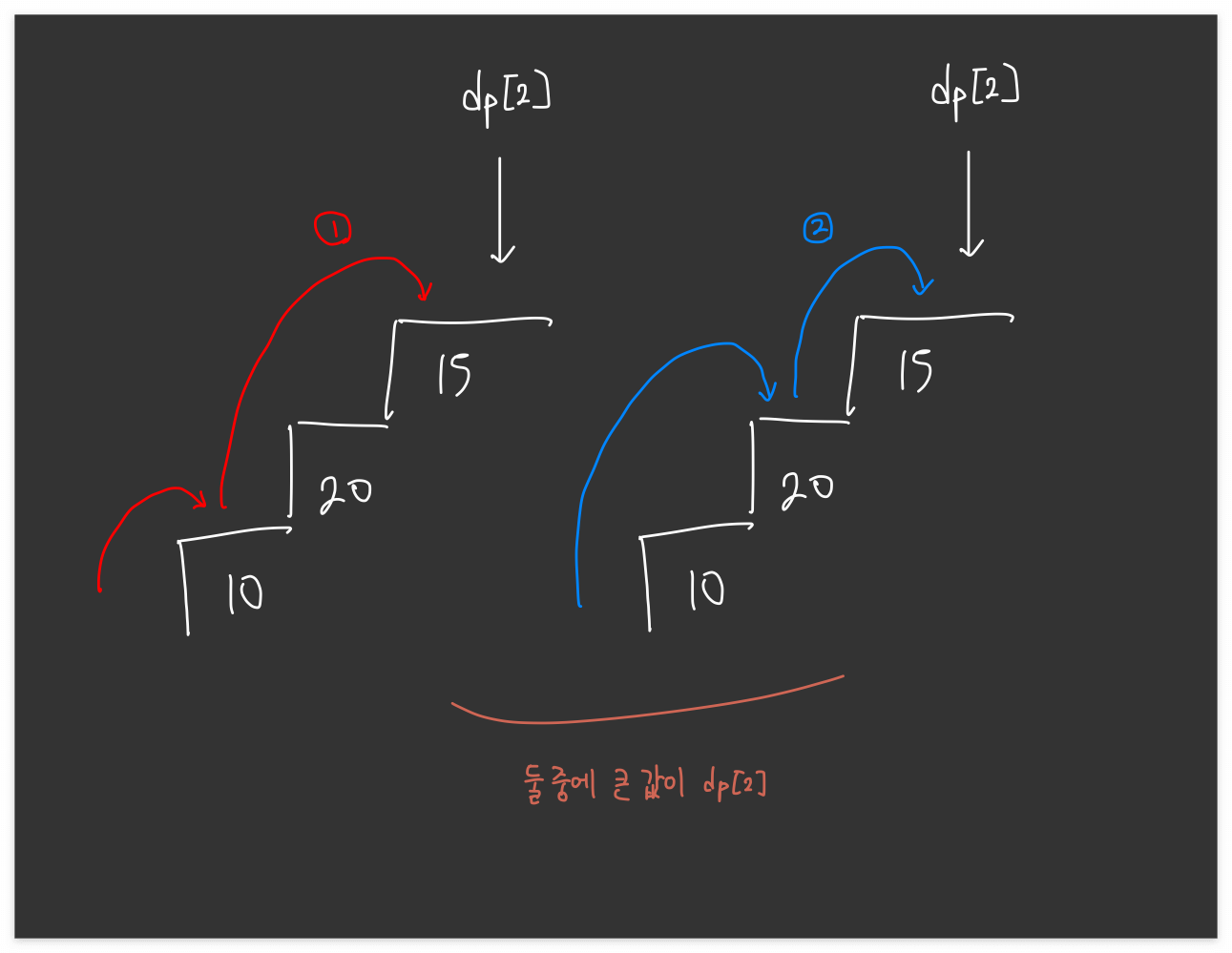
수식은 dp[2] = max(S[0] + S[2], S[1] + S[2]) 입니다.
수식의 일반화
dp[3] 을 생각해 보겠습니다.
dp[3] 으로 올 수 있는 경우의 수는 총 2가지입니다.
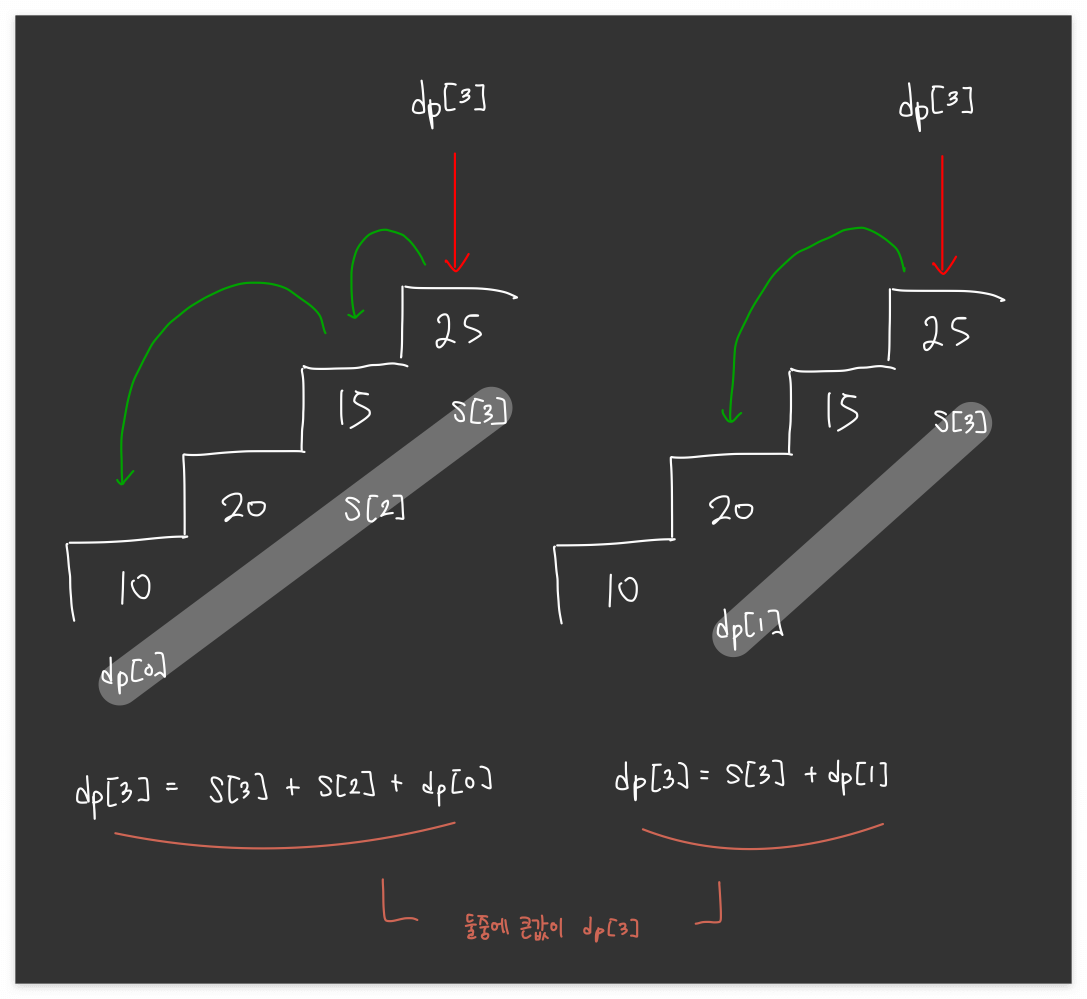
왼쪽경우는 i번째 계단에서 올라오는 첫 번째 경우입니다.
만약에 i번째에 도달했을 때 그전에 i-1 번째에서 왔다고 가정합니다.
그러면 i-2번째에서 올 수 없으므로 dp[0] 에서 한번에 S[i-1]으로 오는 경우의 수밖에 없습니다.
오른쪽 경우는 dp[i-1]에서 바로 오는 경우입니다.
왼쪽 경우와 오른쪽 경우에서의 최댓값이 i번째 계단에서의 dp[i] 가 됩니다.
위 경우를 코드로 일반화를 한다면
for i in 3..<N {
dp[i] = max(S[i] + S[i-1] + dp[i-3], S[i] + dp[i-2])
}위와 같은 식을 완성 할 수 있습니다.
조건에서 주어진 계단의 점수들은 10000 이하의 자연수, 즉 양수라고 생각할 수 있습니다.
따라서 조금 더 정리를 한다면 아래처럼 나타낼 수 있습니다.
for i in 3..<N {
dp[i] = S[i] + max(S[i-1] + dp[i-3], dp[i-2])
}
마지막으로 N 이 1일 때와 2일 때를 분기처리 해준다면 최종 결과를 얻을 수 있습니다.
let N = Int(readLine()!)!
var S: [Int] = []
var dp: [Int] = Array(repeating: 0, count: N)
for _ in 0..<N {
let element = Int(readLine()!)!
S.append(element)
}
dp[0] = S[0]
if N == 1 {
print(dp[0])
} else if N == 2 {
dp[1] = S[0] + S[1]
print(dp[1])
} else {
dp[1] = S[0] + S[1]
dp[2] = max(S[0] + S[2], S[1] + S[2])
for i in 3..<N {
dp[i] = S[i] + max(S[i-1] + dp[i-3], dp[i-2])
}
print(dp[N-1])
}